33. The Critical Section Problem

The problem of controlling concurrent access to shared data was recognized very early. In an [undated lecture]https://www.cs.utexas.edu/users/EWD/translations/EWD35-English.html from 1962 or 1963, Dutch computer scientist Edsger W. Dijkstra described what has come to be known as the critical section problem. Each thread executes some critical section of code that must be guarded against concurrent execution, i.e., only one thread is allowed to be executing in its critical section at any given time. The problem is to design a protocol that threads must execute prior to entering their critical section that will enforce the single-access rule. The term critical section is unfortunately misleading, as it should be obvious that it is the shared data that must be protected from concurrent access, and not the code. Think of the critical section as the code that must execute without interference in order to use the shared data correctly. In the shared counter example, the loop body in the increment_thread() and decrement_thread() functions are the critical sections for the counter variable. To identify the critical sections of code, we need to identify all the cases where shared data must be protected against simultaneous modification or access to prevent race conditions. Note also that the same code can be invoked to operate on different data – for example, deposit() called for account #100 in Thread 1, and deposit() called for account #200 in Thread 2 will not interfere with each other. In this case, we have critical sections for two different resources (i.e., two different bank accounts) and they do not need to be protected from each other.

These ideas will become more concrete by the end of this Chapter, but initially we will reason about a single shared resource (like our counter variable), accessed repeatedly by multiple threads, with some additional code before and after the critical section that does not make any accesses to the shared variable.

33.1. Problem Definition

In its classical form, a solution to the critical section problem must meet the following requirements:

Mutual Exclusion

Only one thread can be executing in its critical section at a time.

Progress

If no thread is executing in its critical section, and some threads want to enter their critical section, then eventually some thread must be granted entry to its critical section. Threads that are executing in their remainder code (i.e., code that is unrelated to the critical section) must not delay threads that want to enter the critical section.

Bounded Waiting (No Starvation)

Once a thread has requested entry to its critical section, there is a limit on how many times other threads are allowed to enter their critical sections ahead of it.

The mutual exclusion requirement is fairly obvious—we want to ensure that only one thread at a time can be manipulating the shared data. The progress requirement disallows solutions that meet the mutual exclusion requirement by not allowing any thread to enter the critical section. Finally, the bounded waiting requirement ensures that every thread has a fair chance to use the shared data.

To these basic requirements, we will add a fourth consideration:

Performance

The overhead of entering and exiting the critical section should be small with respect to the work being done within it.

In some solutions that we will look at the bounded waiting requirement is not met, but it is statistically unlikely in real systems that a thread will be continually passed over in favor of other threads entering the critical section.

We also make a number of assumptions:

1. Each thread is executing at non-zero speed, but we make no assumptions about the relative speed of the threads.

2. We assume that individual machine instructions such as load, store, or add are atomic, meaning that they are indivisible. The execution of multiple threads is interleaved at the level of individual machine instructions. For example, if Thread 1 reads a variable and Thread 2 writes the variable at nearly the same time, then Thread 1 will read either the old value, or the new value, but not some mixture of the old and new values.

3. The operations in each thread are executed in the order that they appear in the program code, and the result of concurrent execution is equivalent to some interleaving of operations from each of the concurrent threads. (Note that this last assumption is not true of modern cpu architectures, but we will omit the topic of memory consistency models for now.)

With these requirements and assumptions in place, we now turn our attention to designing a protocol that threads can use to coordinate their use of shared data. Once we have identified the critical sections, we insert an entry section before the critical section, and an exit section immediately after the critical section. Each thread must request permission to enter its critical section, by executing the protocol in its entry section. When it completes the entry, the thread is guaranteed to have exclusive access to the shared data accessed within the critical section. When it finishes the critical section, the thread executes the code in the exit section to make the critical section available to other threads. Each thread may request entry to its critical section repeatedly. All other code executed by the thread, either before entry to, or after exit from, the critical section will be referred to as the remainder of the code.

Fig. 33.1 illustrates these concepts with a concrete code example from the increment_thread function in the shared counter program. In this figure, we are showing where the entry and exit sections need to be added around the critical section of code that accesses the shared variable, without specifying what goes into those sections.

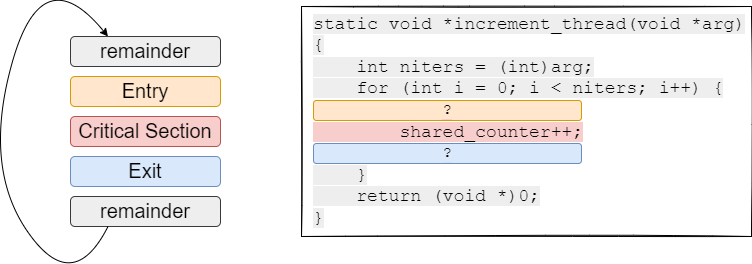
Fig. 33.1 Abstract view of a critical section of code, surrounded by entry and exit sections (left), and example of these concepts in the increment_thread function (right).

33.2. Abstracting the Problem

We can encapsulate solutions to the critical section problem into a lock abstract data type, with the following operations:

• acquire() : Obtain exclusive access to a critical section; this function returns only when the calling thread is granted entry to the critical section.

• release() : Leave the critical region, making it available to other threads.

The lock data type may also have some private data, which can be used by the acquire() and release() functions, but is not otherwise visible. Exactly what this data might be will depend on the implementation of these functions.

We associate a lock object with the shared data that we need to protect. Threads must invoke the lock.acquire() function to enter the critical section, and the lock.release() function to leave the critical section, as shown in Fig. 33.2. Note that we can have multiple lock objects that protect different data objects, such as a separate lock for each bank account. Threads simply simply have to invoke the acquire() and release() operations on the right lock object.

The lock data type is sometimes called a mutex, because it is used to guarantee mutual exclusion, and the operations on a mutex are often called lock() and unlock(), with the same semantics as the acquire and release functions.

Fig. 33.2 e w Encapsulating critical section entry and exit with operations on a lock object.

The pthreads specification includes the pthread_mutex_t data type, and operations pthread_mutex_lock(mutex) and pthread_mutex_unlock(mutex) to acquire and release the mutex, respectively. The code in Listing 33.1 shows how we use the pthreads mutex to protect access to the shared counter variable.

Listing 33.1 Protecting access to the shared counter using a pthread mutex.

#include <pthread.h>
#include <stdlib.h>
#include <sys/types.h>
#include <unistd.h>
#include <string.h>
#include <stdio.h>

pthread_mutex_t mutex = PTHREAD_MUTEX_INITIALIZER;
volatile long shared_counter;

static void *increment_thread(void *arg)
{
    long niters = (long)arg;
    for (int i = 0; i < niters; i++) {
        pthread_mutex_lock(&mutex);
        shared_counter++;
        pthread_mutex_unlock(&mutex);
    }

    return (void *)0;
}

static void *decrement_thread(void *arg)
{
    long niters = (long)arg;

    for (int i = 0; i < niters; i++) {
        pthread_mutex_lock(&mutex);
        shared_counter--;
        pthread_mutex_unlock(&mutex);
    }

    return (void *)0;
}

int main(int argc, char **argv)
{
    pthread_t *tids;
    long niters;
    int nthreads, i;
    
    if (argc != 3) {
        fprintf(stderr,"Usage: %s <num_threads> <num_iters>\n",argv[0]);
        return 1;
    }

    nthreads = atoi(argv[1]);
    niters = atoi(argv[2]);
    shared_counter = 0;
    
    printf("Main thread: Beginning test with %d threads\n", nthreads);
    
    tids = (pthread_t *)malloc(nthreads * sizeof(pthread_t));
    
    /* We create the same number of increment and decrement threads, each doing the same number of iterations. 
     * When all threads have completed, we expect the final value of the shared counter to be the same as its
     * initial value (i.e., 0).
     */
    for (i = 0; i < nthreads; i+=2) {
        (void)pthread_create(&tids[i], NULL, increment_thread, (void *)niters );
        (void)pthread_create(&tids[i+1], NULL, decrement_thread, (void *)niters );
    }
    
    /* Wait for child threads to finish */
    for (i = 0; i < nthreads; i+=2) {
        pthread_join(tids[i], NULL);
        pthread_join(tids[i+1], NULL);
    }
    
    printf("Main thread: Final value of shared counter is %ld\n", shared_counter);

    return 0;
}

Now, let’s try running this code and see if we get the expected final counter value, 0.

That looks a lot better! So, armed with a lock abstraction (called mutex in the pthreads library), we have a working solution to the critical section problem. In the next chapter, we will explore the internal implementation of the acquire() and release() functions.